1. NODAĻA

APGALVOJUMA JĒDZIENS:

ATSEVIŠĶI UN VISPĀRĪGI APGALVOJUMI

Pēc šīs nodaļas satura apgūšanas Jūs būsiet spējīgi droši atšķirt atsevišķus apgalvojumus no vispārīgiem apgalvojumiem. Tāpat Jūs varēsiet pārliecinoši pierādīt vienkāršākus apgalvojumus. Apgalvojumu pierādīšanas grafiskā interpretācija diskrētas lentas veidā palīdzēs Jums apgūt sarežģītāku apgalvojumu tehnoloģiju.

Matemātikā lielu nozīmi piešķir kategoriju jeb jēdzienu viennozīmīgām definīcijām. Katrs sarežģītāks apgalvojums (slēdziens, secinājums) balstās uz vairākiem secīgiem vienkāršākiem apgalvojumiem, kuru patiesums ir "acīmredzams". Nav iespējams izveidot stingru secīgu pierādījumu virkni, ja tajā izmantoti neskaidri vai neviennozīmīgi formulēti jēdzieni. Apgalvojuma jēdziens vispārpieņemtajā nozīmē ir izteikums, kas vispārīgā gadījumā var būt gan patiess, gan nepatiess. Šai studiju kursā lietotais apgalvojuma jēdziens nozīmē izteikumu, par kura patiesumu mums nav ne mazāko šaubu. Matemātikā ļoti stingrus apgalvojumus ar tālu ejošām sekām sauc par teorēmām, kuru patiesums katrā gadījumā ir jāpierāda. Katrs apgalvojums nevar pretendēt uz teorēmas statusu, tomēr katra apgalvojuma patiesums tāpat kā teorēmas gadījumā ir jāpierāda. Apgalvojuma patiesuma pierādījums sastāv no secīgu citu vienkāršāku "acīmredzamu" apgalvojumu (loģisku slēdzienu un/vai secinājumu) virknes. Tā kā mūsu pētījumu galvenie objekti ir skaitļi, tad arī apgalvojumi attieksies uz skaitļiem un to īpašībām. Apgalvojumi var attiekties uz vienu vai vairākiem, vai pat uz bezgalīgi daudziem skaitļiem. Atkarībā no tā apgalvojumus ir mērķtiecīgi iedalīt divās principiāli atšķirīgās kategorijās -

1)Atsevišķi apgalvojumi;

2)Vispārīgi apgalvojumi.

Atsevišķi apgalvojumi satur izteikumus par vienu vai vairākiem galīga skaita objektiem (skaitļiem, priekšmetiem, ģeometriskām figūrām u. tml.), turpretim vispārīgi apgalvojumi parasti satur izteikumus par bezgalīgi daudz objektiem (skaitļiem), kas veido dotajam vispārīgajam apgalvojumam specifisku objektu kopu. Katru vispārīgu apgalvojumu var pārvērst par atsevišķu apgalvojumu, ierobežojot objektu skaitu kopā, tomēr ne katra atsevišķu apgalvojumu virkne var novest pie vispārīga apgalvojuma. Atsevišķu apgalvojumu, kas satur izteikumu par viena objekta kādu no īpašībām, kura patiesums ir "acīmredzams" (aksiomātisks) vai arī tā pierādījums seko pēc elementāru matemātisku darbību izpildīšanas, sauc par vienkāršu jeb elementāru apgalvojumu. Katrs vienkāršs apgalvojums ir arī atsevišķs apgalvojums, bet ne otrādi. Vispārīgu apgalvojumu pierādījumi tiek konstruēti kā atsevišķu un/vai vienkāršu apgalvojumu virkne. Zemāk liela uzmanība tiks veltīta šo apgalvojumu patiesuma pierādīšanas tehnoloģijai (paņēmieniem). Tabulā doti dažādu apgalvojumu piemēri.

1. piemērs.

Atsevišķi apgalvojumi attiecas uz galīga skaita objektiem (skaitļiem) un to īpašībām, tāpēc tos visus pēc kārtas var pārskaitīt, lai tie būtu 10, 100 vai arī vairāk. Citādi tas ir ar vispārīgiem apgalvojumiem, kas satur izteikumus par bezgalīgi daudz objektiem, tāpēc tos visus pēc kārtas fiziski nevar pārskaitīt. Tomēr vispārīgu apgalvojumu var pierakstīt līdzīgi kā atsevišķu apgalvojumu ar tā sauktā parametra palīdzību, ar kuru apzīmē kādu patvaļīgi izvēlētu objektu no atbilstošās bezgalīgās objektu kopas. Ja dotais vispārīgais apgalvojums vienlaicīgi attiecas uz bezgalīgās objektu kopas diviem vai vairākiem objektiem, tad to pierakstam būs jālieto divi vai vairāki parametri. Parametru uzdevums ir pārskaitīt visus bezgalīgās kopas objektus (skaitļu gadījumā tie būs parametru pieļaujamās vērtības). Protams, arī atsevišķu apgalvojumu var pierakstīt ar parametru palīdzību, bet tad parametra pieļaujamās vērtības būs galīgs skaits atbilstoši objektu skaitam. Nereti saliktus atsevišķus apgalvojumus, kuru patiesumu nevar pierādīt uzreiz vienā paņēmienā, bet to var izdarīt ar vienkāršu apgalvojumu galīgu virkni, arī sauc par vispārīgiem apgalvojumiem. Atgriezīsimies vēlreiz pie tabulā dotajiem vispārīgo apgalvojumu piemēriem. 1. piemērā minētos vispārīgos apgalvojumus var pierakstīt šādā formā.

• Ja x ir naturāls skaitlis, kas beidzas ar nulli, tad x dalās ar 5.
• Ja ģeometriska figūra s ir kvadrāts, tad figūras s diagonāles ir perpendikulāras.
• Neviens naturāls skaitlis 2n, kur n=1, 2, 3, ... , nedalās ar 117.

1. zīm.

Parametra x vērtības pirmajā apgalvojumā var būt 10, 20, 30, 40 utt. Ievērojot šīs vērtības vispārīgajā apgalvojumā parametra x vietā, iegūstam šādus atsevišķus apgalvojumus: 10 dalās ar 5, 20 dalās ar 5, 30 dalās ar 5 utt. Skaidrs, ka aplūkojamais vispārīgais apgalvojums ir visu šādu atsevišķu apgalvojumu apvienojums. Līdzīgi atrod parametrus un to pieļaujamās vērtības citos vispārīgajos apgalvojumos.

Vispārīgo apgalvojumu "katrs pozitīvs pāra skaitlis dalās ar 2" var pierakstīt šādi: "ja z ir pozitīvs pāra skaitlis, tad z dalās ar 2". Parametra z vērtības var būt 2, 4, 6 utt. Ievietojot šīs vērtības vispārīgā apgalvojumā parametra z vietā, iegūstam šādus atsevišķus apgalvojumus: 2 dalās ar 2, 4 dalās ar 2, 6 dalās ar 2 utt.

Vispārīgs apgalvojums var būt izteikts arī ar vairākiem parametriem. Piemēram, "ja x un y ir reāli skaitļi, tad x+y=y+x". Tas ir vispārīgs apgalvojums ar diviem parametriem x un y. Katrs no tiem var būt jebkurš reāls skaitlis. Lai pareizi izprastu vispārīgu apgalvojumu, vispirmas jānosaka tā parametri.

Aplūkosim saliktu atsevišķu apgalvojumu "neviens viencipara naturāls skaitlis p nedalās ar 15" Tajā apvienoti šādi vienkārši apgalvojumi: 1 nedalās ar 15, 2 nedalās ar 15, 3 nedalās ar 15, …, 9 nedalās ar 15.

Katru no šiem vienkāršiem apgalvojumiem varam attēlot ar rūtiņu, tad saliktais atsevišķais apgalvojums attēlojas ar "lenti", kas sastāv no 9 rūtiņām (2. zīm.): pirmā rūtiņa atbilst apgalvojumam "1 nedalās ar 15", otrā rūtiņa- apgalvojumam "2 nedalās ar 15" utt.

2. zīm.

Aplūkojiet, piemēram, vispārīgu apgalvojumu "katrs naturāls skaitlis n lielāks nekā 0", kas sastāv no atsevišķiem apgalvojumiem "1>0", "2>0", "3>0" utt., arī var iegūt līdzīgu grafisku attēlojumu. Tikai šajā gadījumā, attēlojot katru atsevišķo apgalvojumu ar rūtiņu, "lente", kas attēlo vispārīgo apgalvojumu, ir bezgalīga uz labo pusi (3. zīm.).

Skaidrs, ka šādā veidā var attēlot jebkuru vispārīgu apgalvojumu, kura parametra vērtību kopa ir galīga ("lente" ir galīga), kā arī jebkuru vispārīgu apgalvojumu, kura parametra vērtības var būt 1, 2, 3, … ("lente"ir bezgalīga).

3. zīm.

4. zīm.

Bezgalīgā lente, kas attēlo vispārīgu apgalvojumu, ir tāda pati kā 3. zīmējumā arī tad, ja parametra vērtību kopa ir, piemēram, 7, 8, 9,…, vai arī visi naturālie skaitļi, sākot ar kādu citu naturālu skaitli. Piemēram, apgalvojumā "katram n-stūrim eksistē punkts tā iekšpusē" parametra n vērtības var būt 3, 4, 5,… . Lentē pirmā rūtiņa atbilst apgalvojumam "katram trijstūrim eksistē punkts tā iekšpusē", otrā rūtiņa- apgalvojumam "katram četrstūrim eksistē punkts tā iekšpusē" utt. (4. zīm.).

Ko nozīmē pierādīt, ka atsevišķs apgalvojums ir patiess, parasti neskaidrības nerada. Piemēram, lai pierādītu apgalvojumu "120 dalās ar 5", pietiek ievērot, ka 120=524.

Ko nozīmē pierādīt, ka patiess ir vispārīgs apgalvojums? Jau atzīmējām, ka vispārīgā apgalvojumā ir apvienoti atsevišķi apgalvojumi, kurus iegūst, ievietojot parametra vietā pieļaujamās vērtības. Tātad pierādīt vispārīgu apgavojumu nozīmē pierādīt visus atsevišķos apgalvojumus, kurus no tā var iegūt, ievietojot parametra vietā pieļaujamās vērtības.

Aplūkosim, piemēram, vispārīgu apgalvojumu "katrs naturāls skaitlis, kas beidzas ar 0, dalās ar 5". Tas sastāv no atsevišķiem apgalvojumiem " 10 dalās ar 5", " 20 dalās ar 5", " 30 dalās ar 5 " utt.

Lai pierādītu, ka patiess ir apgalvojums " katrs naturāls skaitlis, kas beidzas ar 0, dalās ar 5 ", kaut kādā veidā jāpierāda visi atsevišķie apgalvojumi.

No teiktā izriet secinājums: lai pierādītu, ka vispārīgais apgalvojums nav patiess, pietiek konstatēt kaut vienas parametra vērtības eksistenci, ar kuru iegūtais atsevišķais apgalvojums ir nepatiess.

2. piemērs. Aplūkojam vispārīgu apgalvojumu " 2ⁿ lielāks nekā 2n katram naturālam skaitlim n". Ja n=1, tad 21=21, tātad vispārīgais apgalvojums ir nepatiess.

Vispārīga apgalvojuma pierādīšanas gaitu var ilustrēt, izmantojot tā grafisko attēlojumu ar lenti, kas sastāv no rūtiņām. Attēlosim vēl nepierādītus apgalvojumus ar baltiem laukumiem, bet pierādītus- ar melniem. Tad vispārīgais apgalvojums būs pierādīts, ja visa lente, kas to attēlo, būs nokrāsota, resp., nokrāsota būs katra lentes rūtiņa. Bet rūtiņu drīkst aizkrāsot, ja pierādīts tai atbilstošs atsevišķais apgalvojums, ko iegūst no vispārīgā apgalvojuma. Tātad jāpierāda katrs atsevišķs apgalvojums.

Ja vispārīgā apgalvojuma parametru vērtību kopa ir galīga, tad principā ir iespējams uzrakstīt visus atsevišķos apgalvojumus, kurus no tā var iegūt, un katru no tiem pierādīt. Piemēram, apgalvojums "neviens naturāls skaitlis, kas mazāks nekā 100, nedalās ar 117"sastāv no atsevišķiem apgalvojumiem "1 nedalās ar 117", "2 nedalās ar 117"…."99 nedalās ar 117".Tos katru var pierādīt, un līdz ar to būs pierādīts arī vispārīgais apgalvojums.

Grafiskajā interpretācijā tas nozīmētu, ka mēs, pierādījuši apgalvojumu "1 nedalās ar 117", aizkrāsojam pirmo rūtiņu, pierādījuši apgalvojumu "2 nedalās ar 117", aizkrāsojam otro rūtiņu utt. Skaidrs, ka pēc 99 soļiem visas rūtiņas, kas atbilst atsevišķajiem apgalvojumiem, būs aizkrāsotas, t.i., būs nokrāsota visa lente, kas attēlo vispārīgo apgalvojumu.

Bet ko darīt, ja vispārīgā apgalvojuma parametra pieļaujamo vērtību ir bezgalīgi daudz? Tādā gadījumā visus atsevišķos apgalvojumus nevar nemaz pierakstīt, kur nu vēl katru no tiem pierādīt. Tomēr šādi vispārīgi apgalvojumi sastopami ļoti bieži. Piemēram: "katram naturālam n skaitlis n(n+1) dalās ar 2"; "ja a, b, c- pozitīvi skaitļi un a=b+c, tad a²>b²+c²"; "katra trijstūra laukums vienāds ar tā pamata un augstuma reizinājuma pusi".

Bieži šādus apgalvojumus pierāda "uzreiz vispārīgā veidā". Piemēram, otro no iepriekš minētajiem apgalvojumiem pierāda tā: ja a=b+c, tad a²=b²+2bc+c², tātad a²-(b²+c²)=2bc. Tā kā b>0 un, c>0, tad 2bc>0. Tātad a²-(b²+c²)>0, tāpēc arī a²>b²+c². Tā kā šie spriedumi ir pareizi jebkurām pozitīvām parametru a, b, c vērtībām, tad apgalvojums pierādīts.

Tomēr nav grūti atrast tādu vispārīgu apgalvojumu piemērus, kurus šādi pierādīt nevar vai vismaz tāds pierādījums ir grūti ieraugāms.

Tāds, piemēram, ir vispārīgais apgalvojums "visiem naturāliem n ir pareiza vienādība

".

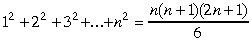Viena no izplatītākajām kļūdām ir apmēram šāds apgalvojuma "pierādījums":

"ja n=1, tad vienādība pareiza, jo

;

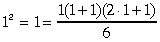ja n=2, tad vienādība pareiza, jo

;

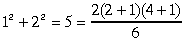ja n=3, tad vienādība pareiza, jo

;

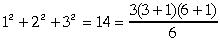redzam, ka vienādība ir pareiza visiem n. Tātad apgalvojums ir patiess."

Nav grūti redzēt šāda "pierādījuma" trūkumu. Īstenībā risinātājs ir pierādījis tikai trīs atsevišķus apgalvojumus:

,

un no tā, ka šie apgalvojumi ir patiesi, izdarījis secinājumu, ka ir patiess vispārīgais apgalvojums. Bet mēs jau atzīmējām, ka vispārīgais apgalvojums ir pierādīts tikai tad, kad ir pierādīti visi atsevišķie apgalvojumi, kurus no tā var iegūt, piešķirot parametrriem konkrētas skaitliskas vērtības. Tā kā risinātājs neko nenoskaidro par atsevišķajiem apgalvojumiem, kurus var iegūt, piešķirot parametram n citas naturālas vērtības, tad viņa vārdi "redzam, ka vienādība ir pareiza visiem n" ir nepamatoti, un viņam nav tiesību apgalvot, ka vispārīgais apgalvojums ir pierādīts.

Grafiskajā interpretācijā ar kvadrātiņiem un lentēm tas redzams ļoti uzskatāmi. Aplūkojamo apgalvojumu var attēlot ar bezgalīgu lenti. Minētā sprieduma autors ir pierādījis tikai atsevišķos apgalvojumus ar n=1, 2, 3, tāpēc viņam ir tiesības iekrāsot lentes pirmās 3 rūtiņas, bet visas pārējās rūtiņas paliek baltas. Līdz ar to vispārīgais apgalvojums nav pierādīts- tas būtu pierādīts, ja visa lente būtu nokrāsota (5. zīm.).

5. zīm.

"Bet", varbūt iebildīs lasitājs, kas pārbaudījis vēl dažus atsevišķus apgalvojumus (ja n=4, 5, 6 un 7 vai vēl vairāk) un pārliecinājies par to pareizību, "vai tad var būt tā, ka vispārīgais apgalvojums, kas patiess ar daudzām atsevišķām parametra vērtībām, pēkšņi dažām parametra vērtībām nav patiess?"

Izrādās, ka tā var būt, un pat ļoti bieži.

3. piemērs. Apskatīsim apgalvojumu "neviens naturāls skaitlis, kura decimālajā pierakstā ir tikai vieninieki, nedalās ar 7".

To var pierakstīt šādi: "vesels pozitīvs skaitlis, kura decimālais pieraksts sastāv no n vieniniekiem (n- jebkurš naturāls skaitlis), nedalās ar 7". Ja n=1, tad apgalvojums ir patiess, jo 1 nedalās ar 7. Ja n=2, tad apgalvojums ir patiess, jo 11 nedalās ar 7. Patiesi ir arī atsevišķie apgalvojumi, kurus iegūst, ja n=3, 4, 5. Bet, ja n=6, apgalvojums "111111 nedalās ar 7" ir nepatiess, jo 111111=715873, un tātad ir nepatiess arī vispārīgais apgalvojums.

6. zīm.

Grafiski tas nozīmētu, ka rūtiņa, kas atbilst atsevišķam apgalvojumam n=6, paliek balta, līdz ar to visu rūtiņu rindu aizkrāsot nevar (6. zīm.).

4. piemērs. Apskatīsim apgalvojumu "nevienam naturālam n skaitlis 3n+4 nedalās ar 17."

Atsevišķie apgalvojumi ir patiesi, ja n=1, 2,… 9, bet, ja n=10, apgalvojums nav patiess: 310+4=34=217.

Šoreiz neaizkrāsota paliek rūtiņa, kas atbilst apgalvojumam ar parametra vērtību 10.

5. piemērs. Apskatīsim apgalvojumu "katram naturālam n ir pareiza nevienādība

.

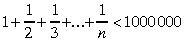Ja sāksiet pārbaudīt šīs nevienādības pareizību n vērtībām 1, 2, 3 utt., tad savas dzīves laikā nepatiesu nevienādību neatradīsiet. Un tomēr to var pierādīt, ka, piemēram,

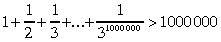
(sk.184. uzdevuma risinājumu).

No šiem piemēriem jāizdara viens svarīgs secinājums.

Pieņemsim, ka aplūkojamā vispārīgā apgalvojuma parametra vērtību kopa ir bezgalīga. Ja esam pierādījuši patiesumu kaut kādam galīgam skaitam atsevišķo apgalvojumu, kurus iegūst no šī vispārīgā apgalvojuma, ievietojiet parametra vietā konkrētus skaitļus, tad tas vien vēl nenozīmē, ka vispārīgais apgalvojums ir patiess.

Bet ko darīt ar vispārīgiem apgalvojumiem, kuriem atrast pierādījumu "uzreiz vispārīgā veidā" neizdodas?

Uzdevumi paškontrolei I

1. Norādīt parametrus un to pieļaujamās vērtības šādos vispārīgos apgalvojumos:

a) katrs naturāls skaitlis n dalās ar 1;

b)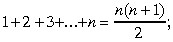

c)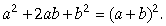

2. Apzīmējot parametrus ar burtiem un norādot to pieļaujamās vērtības, formulēt šādus apgalvojumus:

a) no katra pozitīva skaitļa var izvilkt kvadrātsakni;

b) divu skaitļu reizinājums nemainās, ja maina reizinātāju kārtību.

3. Norādīt, kādi atsevišķi apgalvojumi apvienoti šādā vispārīgā apgalvojumā:

a) katram naturālam n ir pareiza vienādība n²=nn;

b) neviens naturāls skaitlis, kas mazāks nekā 10, nav lielāks kā 20.

4. Pierādīt, ka vispārīgs apgalvojums "2ⁿ lielāks nekā n2 katram naturālam n "ir aplams.