2. NODAĻA

ATSEVIŠĶU APGALVOJUMU PAKĀPENISKA PIERĀDĪŠANA

Pēc šīs nodaļas satura apgūšanas Jūs varēsiet pārliecinoši pierādīt sarežģītu vai saliktu atsevišķu apgalvojumu patiesumu. Sevišķi noderīga Jums izrādīsies apgalvojumu patiesuma pierādīšanas tehnoloģijas apgūšana. Jūs pašiem nemanot jau intuitīvi būsiet apguvuši matemātiskās indukcijas metodi, kas māca, kā no atsevišķiem faktiem un kopsakarībām nonākt līdz vispārīgām likumsakarībām.

Pieņemsim, ka kādam sportistam ir uzdevums- aizlēkt tālumā 7 metrus. Ja viņš ir starptautiskas klases sporta meistars tāllēkšanā, tas viņam sevišķas grūtības nesagādās; ja turpretī viņš ar tāllēkšanu iepriekš nav nodarbojies, tad mēģinājums veikt uzdevumu uzreiz nevar beigties citādi kā ar neveiksmi. Acīmredzot, lai izpildītu šo atsevišķo uzdevumu, sportists trenēsies un vispirms aizlēks tālumā 3 m, pēc tam 4 m, 5 m, 6 m, un tikai tad ķersies pie sākotnējā uzdevuma- aizlēkt 7 m tālu.

Līdzīga situācija bieži gadās matemātikā: lai atrisinātu kādu atsevišķu problēmu, tiek aplūkota problēmu virkne. Risinot citu pēc citas šīs virknes problēmas, galu galā nonākam pie mūs interesējošās problēmas atrisinājuma.

6. piemērs. Pierādīt, ka skaitli 12 var tieši 233 veidos izteikt ar vieninieku un divnieku summu, ja izteiksmes, kas atšķiras tikai ar saskaitāmo kārtību, uzskata par dažādām. (Piemēram, skaitli 3 tā var izteikt trijos veidos: 3=1+1+1=1+2=2+1.)

Protams, mēs varētu mēģināt uzrakstīt visas iespējamā skaitļa 12 izteiksmes ar vieninieku un divnieku summu, un pēc tam saskaitīt, cik tādu izteiksmju ir. Tomēr tam vajadzētu daudz laika, un būtu ļoti jāuzmanās, lai kāda no iespējām nepaliktu nepamanīta. Tāpēc rīkosimies citādi: mēģināsim pakāpeniski noskaidrot, cik dažādos veidos ar vieninieku un divnieku summu izsakāmi skaitļi 1, 2, 3, 4,…, un centīsimies ieraudzīt iegūto rezultātu veidošanās likumību.

Skaitli 1 ar minētā veida summu var izsacīt tikai vienā veidā: 1=1;

skaitli 2- divos veidos: 2=2=1+1;

skaitli 3, kā to jau redzējām,- trijos veidos;

skaitli 4- piecos veidos: 4=1+1+1+1=1+1+2=1+2+1=2+1+1=2+2;

skaitli5-astoņosveidos:5=1+1+1+1+1=1+1+1+2=1+2+1+1=1+1+2+1=

=2+1+1+1=2+2+1=2+2+1=1+2+2.

To dažādo summu skaitu, kas saskaņā ar uzdevuma nosacījumiem izsaka skaitli n, apzīmēsim ar A(n). Iegūstam tabulu (7. zīm.).

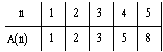
7. zīm.

Nav grūti arī aprēķināt, ka A(6)=13. Redzam, ka šīs tabulas apakšējā rindiņā katrs skaitlis, sākot ar trešo, ir divu iepriekšējo skaitļu summa. Tā nav nejaušība, bet vispārēja likumsakarība: visiem naturāliem n

A(n+2)=A(n)+A(n+1).

(1)

Tiešām, pēc definīcijas skaitli n+2 var uzrakstīt ar vieninieku un divnieku summu A(n+2) dažādos veidos. Katra šāda summa sākas vai nu ar saskaitāmo 1 (sauksim tādas summas par summām), vai ar saskaitāmo 2 (sauksim tādas summas par summām). Katrai summai pārējo saskaitāmo summa (bez pirmā vieninieka) ir n+1, un šie pārējie saskaitāmie ir 1 vai 2, tātad summu skaits ir A(n+1). Līdzīgi secina, ka summu skaits ir A(n). Tā kā katra summa atšķiras no katras summas jau ar pirmo saskaitāmo, tad vienādība (1) tiešām ir pareiza.

Tagad, izmantojot vienādību (1), atrodam, ka A(6)=A(5)+A(4)=13, A(7)=A(6)+A(5)=21, A(8)=21+13=34, A(9)=55, A(10)=89, A(11)=144, A(12)=233, ko arī vajadzēja pierādīt.

7. piemērs. Aprēķināt vieninieku skaitu, kas izmantoti par saskaitāmajiem, visos iespējamajos veidos izsakot skaitli 12 ar vieninieku un divnieku summu.

Lietosim tādus pašus apzīmējumus kā 6. piemērā. Bez tam ar S(n) apzīmēsim vieninieku skaitu, kas izmantoti par saskaitāmajiem, visos iespējamos veidos izsakot n ar vieninieku un divnieku summu. No 6. piemēra risinājuma redzams, ka S(1)=1, S(2)=2, S(3)=5, S(4)=10, S(5)=20. Analizēsim saknes S(n) veidošanās procesu.

Skaitli n+2 saskaņā ar 6. piemēra nosacījumiem var izsacīt ar summām un summām. Katrai summai pirmais saskaitāmais ir vieninieks; tā kā summu skaits ir A(n+1), tad šādu vieninieku- pirmo saskaitāmo- A(n+1). Nosvītrojot katrai summai pirmo vieninieku, iegūstam visas skaitļa n+1 izteiksmes ar vieninieku un divnieku summām; saskaņā ar S(n) definīciju tās satur S(n+1) vieniniekus.

Tātad visās summās, kas izsaka skaitli n+2, kopā ir A(n+1)+S(n+1) vieninieki.

Līdzīgi pierāda, ka visās summās, kas izsaka skaitli n+2, kopā ir S(n) vieninieki. Tāpēc

S(n+2)=S(n)+S(n+1)+A(n+1).

(1)

Saskaņā ar formulu (1) varam pakāpeniski aizpildīt tabulu 8. zīmējumā (A(n) vērtību rindiņa ņemta no 6. piemēra)

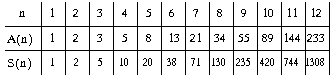
8. zīm.

8. piemērs. Cik ir tādu 8-ciparu naturālu skaitļu, kuru decimālais pieraksts sastāv no cipariem 1, 2 un 3 un kuriem ik divu blakus ciparu starpība nepārsniedz 1?

Apzīmēsim ar A(n), B(n), C(n) to n-ciparu skaitļu kopu, kuru decimālais pieraksts sākas ar ciparu 1 (ar 2, ar 3), kuri sastāv no cipariem 1, 2, un 3 un kuriem ik divus blakus ciparu starpība nepārsniedz 1. Ar a_n, b_n, un c_n apzīmēsim šo kopu elementu skaitu, ar S_n- visu uzdevumā minēto skaitļu skaitu.

Nosvītrojot kādam kopas A(n+1) elementam pirmo ciparu (vieninieku), mēs iegūstam vai nu kopas A(n), vai kopas B(n) elementu. Otrādi, katram kopas A(n) vai kopas B(n) elementam pierakstot priekšā vieninieku, iegūstam A(n+1) elementu. Turklāt, veicot šīs operācijas, no dažādiem skaitļiem iegūstam dažādus skaitļus. Tātad

an+1=an+bn

(1)

Līdzīgi iegūstam formulas

bn+1=an+bn+cn	(2)
cn+1=bn+cn.	(3)

Tā kā a₁=b₁=c₁=1, tad izmantojot formulas (1)-(3), pakāpeniski izveidojam tabulu (9. zīm.).

Iegūstam, ka S₈=a₈+b₈+c₈=1393

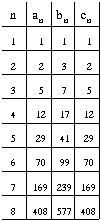
9. zīm.

9. piemērs. Pieņemsim, ka rindā uzzīmēti 7 balti aplīši. Pirmajā minūtē nokrāsojam vienu no tiem (vienalga, kuru); rindā paliek viens vai divi "bloki", kas sastāv no baltiem aplīšiem. Otrajā minūtē katrā blokā nokrāsojam pa vienam baltam aplītim; rindā rodas vairāki bloki, kas sastāv no baltiem aplīšiem. Tā turpinām, kamēr visi aplīši nokrāsoti.

Cik dažādos veidos šo procesu iespējams realizēt?

Uzzīmēsim rindā n baltus aplīšus un apzīmēsim krāsošanas dažādo realizāciju skaitu ar A(n). Acīmredzot A(1)=1, A(2)=2, A(3)=5.

Ja pirmajā minūtē nokrāso pirmo aplīti, tad rindā paliek viens bloks, kas sastāv no (n-1) baltiem aplīšiem. Šī bloka krāsošnu acīmredzot var turpināt A(n-1) veidos.

Ja pirmajā minūtē nokrāso otro aplīti, tad rindā paliek divi bloki: viens sastāv no viena aplīša, otrs- no (n-2) aplīšiem. Pirmā bloka krāsošanu var turpināt A(1) veidos, otrā bloka krāsošanu- A(n-2) veidos. Katrs pirmā bloka krāsošanas veids var kombinēties ar otrā bloka krāsošanas veidu, tāpēc pavisam dažādu turpinājumu ir A(1)A(n-2).

Pieņemsim, ka pirmajā minūtē mēs nokrāsojam k-to aplīti, 2kn-1. Spriežot tāpat kā iepriekš, konstatējam, ka procesu var turpināt A(k-1)A(n-k) dažādos veidos.

Ja pirmajā minūtē iekrāso n-to aplīti, tad dažādu turpinājumu ir A(n-1).

Divi krāsošanas veidi, kas atšķiras viens no otra jau pirmajā solī, ir dažādi, tāpēc iegūstam formulu

un no šīs formulas savukārt

ko arī vajadzēja aprēķināt.

10. piemērs. Funkcijas f(x) un g(x) definētas naturālo skaitļu kopā un tām ir šādas īpašības:

1. f(1)<f(2)<f(3)…;
2. g(1)<g(2)<g(3)…;
3. f un g vērtības ir naturāli skaitļi;
4. f un g vērtību kopām nav kopēju elementu;
5. f un g vērtību kopu apvienojums ir visa naturālo skaitļu kopa;
6. katram naturālam n

g(n)=f(f(n))+1.

Aprēķināt f(56).

No nosacījumiem f) un c) izriet, ka g(n)>1 katram naturālam n. Tāpēc no nosacījumiem e) un a) secinām, ka f(1)=1; tad g(1)=f(f(1))+1=f(1)+1=2. Ievērojot nosacījumus a) un d), iegūstam, ka f(2)3 Tādēļ nosacījuma a) viegli secināt, ka f(n)>n, ja n>1. Bet tad g(n)=f(f(n))+1>f(f(n))f(n) , tātad visiem naturāliem n ir pareiza nevienādība

g(n)>f(n).

(1)

Aplūkosim naturālos skaitļus no intervāla [1, g(n)-1]. Tā kā g(n)-1=f(fn)), tad šajā intervālā atrodas skaitlis f(f(n)); tā kā f(t)- monotoni augoša funkcija, tad intervālā [1, g(n)-1].atrodas arī visi skaitļi f(1), f(2), f(3), …,f(f(n)-1), tātad šajā intervālā atrodas f(n) funkcijas f vērtību. Tā kā g(t)- monotoni augoša funkcija, tad minētajā intervālā atrodas vērtības g(1), g(2), …, g(n-1), tātad (n-1) funkcijas g vērtības. Ievērojot nosacījumus d) un e), iegūstam, ka f(n)+n-1=g(n)-1, jo katrs no apskatāmajā intervālā ietilpstošajiem g(n)-1 naturālajiem skaitļiem pieder tieši pie vienas no kopām

Tā kā f(n)+n-1=g(n)-1=f(f(n)), tad

f(f(n))=f(n)+n-1.

No nosacījuma (1) un no tā, ka f(1)=1, g(1)=2, viegli iegūst, ka f(2)=3. Tāpēc

f(3)=f(f(2))=f(2)=2-1=3+2-1=4,

f(4)=f(f(3))=f(3)+3-1=4+3-1=6,

f(6)=9, f(9)=14, f(14)=22, f(22)=35, f(35)=56, f(56)=90,

ko arī vajadzēja aprēķināt.

11. piemērs. Pilsēta sastāv no 55 kvadrātveida kvartāliem (10. zīm.). Ielas tajā vērstas ziemeļu-dienvidu un austrumu-rietumu virzienā. Pa cik dažādiem ceļiem iespējams aiziet no punkta A uz punktu B, neejot uz dienvidiem un uz rietumiem?

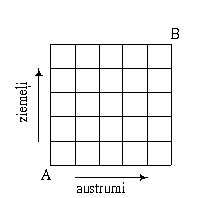
10. zīm.

Aprēķināsim pakāpeniski visiem pilsētas ielu krustojumiem, pa cik ceļiem tajos var nokļūt no punkta A, neejot dienvidu un rietumu virzienā.

Krustojumam K apzīmēsim šo ceļu skaitu ar (K).

Skaidrs, ka (A)=1, jo no A uz A saskaņā ar uzdevuma nosacījumiem var "nonākt" tikai vienā veidā- paliekot uz vietas.

Ja krustojumam Z eksistē blakus krustojums gan pa kreisi gan uz leju (11. zīm. a), tad

(Z)=(X)+(Y).

(1)

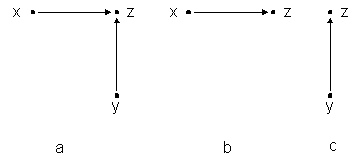
11. zīm.

Tiešām, krustojumā Z var nonākt vai nu no krustojuma X, vai no krustojuma Y, tātad vai nu turpinot ceļu, kas noved uz X, vai turpinot ceļu, kas noved uz Y.

Ja krustojumam Z nav vai nu krustojuma uz leju (11. zīm. b), vai krustojuma pa kreisi (11. zīm. c), tad līdzīgi iegūstam, ka

(Z)=(X) vai	(2)
(Z)=(Y).	(3)

Formulas (2) un (3) atkārtoti lietojot, atrodam, ka visiem krustojumiem, kas atrodas uz vienas horizontāles vai vertikāles ar A, meklējamais ceļu skaits arī ir 1 (12. zīm.).

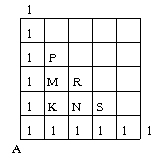
12. zīm.

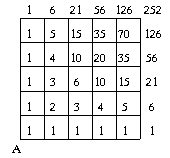
13. zīm.

Pēc tam lietojot formulu (1), pakāpeniski atrodam (vērtības visos pārējos krustpunktos: vispirms punktā K, tad tad punktos M un N, pēc tam punktos P, R un S utt. Iegūtie rezultāti attēloti 13. zīmējumā. tātad (B)=252.

Uzdevumi paškontrolei II

5. Kāpnēm ir 15 pakāpieni. Cik veidos pa tām var uzkāpt, ja ar vienu soli var pārvarēt vai nu 1, vai 2 pakāpienus?

6. Cik dažādos veidos rindā var nostādīt 10 skolēnus, ja nekādas divas meitenes nedrīkst stāvēt blakus? Divus veidus uzskata par dažādiem tad un tikai tad, ja vienā no tiem kādā vietā stāv meitene, bet otrā- tai pašā vietā stāv zēns.

7. Cik dažādos veidos skaitli 15 var izteikt ar divnieku un trijnieku summu? Summas, kas atšķiras tikai ar saskaitāmo kārtību, uzskata par dažādām.

8. Cik divnieku izmantoti par saskaitāmajiem, visos iespējamajos veidos izsakot skaitli 12 ar vieninieku un divnieku summu? Summas, kas atšķiras tikai ar askaitāmo kārtību, uzskata par dažādām.

9. Cik "+" zīmes izmantotas, visos iespējamos veidos izsakot skaitli 12 saskaņā ar 8. uzdevuma nosacījumie?

10. Seši cilvēki atnāca uz viesībām un katrs pakāra priekšnamā savu cepuri. Kad viņi gatavojās doties mājās, priekšnamā nodzisa gaisma, un katrs tumsā paņēma vienu no cepurēm. Cik veidos viņi varēja paņemt cepures tā, lai neviens nepaņemtu savu cepuri?

11. Uz riņķa līnijas atzīmēti 12 punkti. Tie pa pāriem jāsavieno ar nogriežņiem tā, lai nekādiem diviem nogriežņiem nebūtu kopīgu punktu. Cik veidos iespējams to izdarīt?

12. Regulāra astoņstūra virsotnē A atrodas ķengurs, bet virsotnē E- krātiņš (14. zīm.). Ar vienu lēcienu ķengurs var pārvietoties no virsotnes, kurā atrodas, uz vienu (vienalga, kuru) no divām blakus virsotnēm. Ja ķengurs nonāk krātiņā, tā durvis automātiski aizcērtas, un turpināt lēcienus ķengurs vairs nevar. Cik dažādos veidos ķengurs var nonākt krātiņā, izdarot tieši 12 lēcienus?

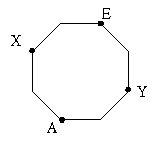
14. zīm.

13. Abi auklas gredzeni, kas attēloti 15. zīmējumā, nav atbrīvojami viens no otra. Tomēr, pārgriežot jebkuru no tiem, gredzenus var atbrīvot vienu no otra.

Savienot sešus auklas gredzenus tā, lai tie nebūtu atbrīvojami cits no cita, bet pārgriežot vienu (vienalga, kuru) no tiem, visus gredzenus varētu atbrīvot citu no cita.

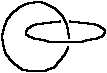
15. zīm.

*14. Pierādīt, ka 10. piemērā aplūkotajām funkcijām f(x) un g(x) ir pareizas vienādības f(n)=[n] un g(n)=[n²], kur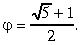

*15. Pierādīt, ka 10. piemērā aplūkotajām funkcijām f(x) un g(x) ir pareiza vienādība

*16. Pierādīt, ka 10. piemērā aplūkotajām funkcijām f(x) un g(x) ar visiem naturāliem n ir pareizas vienādības

kur (a_n)- Fibonači virkne (sk. 21. lpp.).

*17. Apzīmēsim ar x_n visu n-cipru naturālo skaitļu skaitu, kuru decimālais pieraksts satur tikai ciparus 1, 2,un 3 un kuriem ik blakus ciparu starpība nepārsniedz 1. (Skaidrs, ka x₁=3, x₂=7.)

Pierādīt, ka visiem naturāliem n ir pareiza vienādība

*18. (Tēma skolēnu zinātniskajai biedrībai.)

Aplūkosim līdz ar Fibonači virkni arī t.s. Lukasa virkni, kuru definē šādi

Atrast sakarības, kas saista Lukasa skaitļus ar 10. piemērā aplūkotajām funkcijām f(x) un g(x).

Ko vēl jūs noskaidrojāt par Fibonači skaitļu, Lukasa skaitļu un 10. piemēra funkciju savstarpējām sakarībām?

*19. Izmantojot 7. piemēra un 8. uzdevuma risinājumus un apzīmējumus, pierādīt, ka

kur T(m)- divnieku skaits, kas izmantoti par saskaitāmajiem, visos iespējamos veidos izsakot skaitli m saskaņā ar 6. piemēra nosacījumiem.

Vai varat šo vienādību pierādīt tieši?

*20. Pierādīt, ka veidu skaits, kuros n cilvēki var pilnīgi sajaukt cepures (sk. 10. uzdevumu), ir

*21. Pierādīt, ka to veidu skaits, kuros no nogriežņiem var savienot 2n punktus (sk. 11. uzdevumu), ir

.

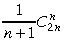ĪSS LITERATŪRAS APSKATS

Šajā paragrāfā izmantotā rekurento sakarību metode matemātikā ir ļoti svarīga un plaši lietota. Daudzus ar tās palīdzību risināmus uzdevumus var atrast grāmatā [1]; darbā [2] šī metode izklāstīta sistemātiski un izvērsti. 11. piemērā aplūkotais divdimensionālais skaitļu masīvs cieši saistīts ar Paskāla trijstūri; par tā īpašībām sk., piemēram, grāmatas [3], [4] un rakstus [5], [6].