
| 
| 
| 
| 
|

| 
| 
| 
| 
|
11. NODAĻA
INDUKCIJAS IZMANTOŠANA ALGORITMU PAREIZĪBAS PIERĀDĪŠANĀ
(INDUKCIJAS METODES PIELIETOJUMI)
| Matemātiskās indukcijas pielietošanas iespējas ir ļoti plašas. Šajā nodaļā Jūs studēsiet piemērus, kuros indukcija galvenokārt tiek izmantota, pierādot dažādu doto algoritmu pareizību. Jūs varēsiet pārliecināties, ka algoritmu pareizības pierādīšana atšķiras no iepriekš plaši praktizētās apgalvojumu patiesuma pierādīšanas. |
Lielāko daļu līdz šim aplūkoto piemēru un uzdevumu var iedalīt vienā no trim grupām:
Iepriekš apskatītie c) tipa piemēri bija tādi, kuros indukcija galvenokārt tika izmantota pašu algoritmu aprakstīšanai; aprakstīto algoritmu pareizība pēc to konstrukcijas bija acīmredzama.
Šajā nodaļā mēs apskatīsim piemērus,
kuros indukcija galvenokārt tiek izmantota, pierādot
aprakstīto algoritmu pareizību.
85. piemērs. Konfekšu kaudzītē ir n konfektes. Divi spēlētāji A un B pēc kārtas izdara pa vienam gājienam; pirmo gājienu izdara spēlētājs A. Ar vienu gājienu katra kaudzīte, kurā ir vairāk nekā viena konfekte, jāsadala divās mazākās kaudzītēs, kas katra sastāv no vesela skaita (varbūt vienas pašas) konfekšu. Zaudē tas spēlētājs, kurš nevar izdarīt gājienu. Kādām n vērtībām A var uzvarēt? Kā jāspēlē, lai uzvarētu?
Pierādīsim šādu teorēmu.
I teorēma. Ja n2k-1, tad spēlētājs A var uzvarēt. Lai uzvarētu, viņam katrā savā gājienā jāsadala kaudzītes tā, lai vislielākajā kaudzītē konfekšu skaits būtu 2l-1.
Ja n=2k-1, tad pareizi spēlējot, var uzvarēt spēlētājs B (k un l- naturāli skaitļi).
Definēsim spēles stāvokļa jēdzienu. Ja uz galda atrodas m kaudzītes konfekšu, kas satur attiecīgi k1, k2, …, km konfektes, tad sacīsim, ka spēle atrodas stāvoklī <k1, k2, …, km>, turklāt pieņemsim, ka k1 nav mazāks kā katrs no skaitļiem k2, …, km.
Acīmredzot sākumā spēle atrodas stāvoklī <n>. Uzvar tas spēlētājs, pēc kura gājiena spēles stāvoklis ir <1; 1;…; 1>, jo tad visas kaudzītes satur pa vienai konfektei un pretiniekam nav iespējams izdarīt gājienu.
Pierādīsim vispārīgāku teorēmu.
II teorēma. Spēlētājs, kuram jāizdara gājiens, kad spēle ir stāvoklī <k1; k2; …; km>, var uzvarēt ja k12l-1, lN. Lai uzvarētu, viņam spēle jānoved (un viņš to var izdarīt) stāvoklī <k'1; k'2;…; k'm1>, kur k'1=2l-1, lN; spēlētājs, kam jāizdara gājiens, kad spēle ir stāvoklī <k1; k2; …; km>, kur k1=2l-1, lN, nevar uzvarēt, ja pretinieks spēlē pareizi.
Pielietojot šo teorēmu spēlei, kas ir stāvoklī <n>, iegūstam I teorēmu (m=1, k1=n).
Pierādīsim II teorēmu ar indukciju pēc k1.
Bāze. Ja k1=1, tad k1=k2=…=km=1, spēlētājs A nevar izdarīt gājienu un tātad zaudē. Tas saskan ar teorēmas apgalvojumu, jo k1=1=21-1.
Ja k1=2, tad dažās kaudzītēs ir 2 konfektes, bet dažās citās (ja tādas ir)- tikai viena konfekte. Spēlētājs A var uzvarēt, sadalot katru kaudzīti, kurā ir 2 konfektes, divās kaudzītēs pa vienai konfektei katrā. Tas saskan ar teorēmas apgalvojumu, jo 22l-1, lN, un pēc spēlētāja A gājiena konfekšu skaits lielākajā kaudzītē ir 21-1.
Pāreja "<nn", ja n3. Pieņemsim, ka teorēma jau pierādīta, ja k1=1, k1=2…, k1=n-1. Pierādīsim to, ka ja k1=n. Šķirosim divus gadījumus.
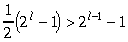 konfektes. Tātad
pēc spēlētāja A gājiena
vislielākajā kaudzītē konfekšu skaits
būs lielāks nekā 2l-1-1,
bet mazāks nekā 2l-1, jo pirms pēdējās
dalīšanas nevienā kaudzītē nebija
vairāk kā 2l-1 konfektes, un katrā
kaudzītē ar vairāk nekā vienu konfekti
pēc spēlētāja A gājiena
to skaits samazinājās. Tātad pēc spēlētāja
A gājiena spēles stāvoklis ir <k'1;
k'2;…; k'm1>,
kur k'1=2l-1-1<k'1<2l-1,
t.i., k'12ss, sN.
Tā kā k'1<n,
tad pēc induktīvā pieņēmuma
spēlētājs, kuram šjā stāvoklī
jāizdara gājiens, t.i., spēlētājs
B, var uzvarēt, ko arī vajadzēja pierādīt;
spēlētājs A zaudēs, ja B
spēlēs pareizi
konfektes. Tātad
pēc spēlētāja A gājiena
vislielākajā kaudzītē konfekšu skaits
būs lielāks nekā 2l-1-1,
bet mazāks nekā 2l-1, jo pirms pēdējās
dalīšanas nevienā kaudzītē nebija
vairāk kā 2l-1 konfektes, un katrā
kaudzītē ar vairāk nekā vienu konfekti
pēc spēlētāja A gājiena
to skaits samazinājās. Tātad pēc spēlētāja
A gājiena spēles stāvoklis ir <k'1;
k'2;…; k'm1>,
kur k'1=2l-1-1<k'1<2l-1,
t.i., k'12ss, sN.
Tā kā k'1<n,
tad pēc induktīvā pieņēmuma
spēlētājs, kuram šjā stāvoklī
jāizdara gājiens, t.i., spēlētājs
B, var uzvarēt, ko arī vajadzēja pierādīt;
spēlētājs A zaudēs, ja B
spēlēs pareizi
Ja n=k12l-1, lN tad eksistē tāds naturāls skaitlis s, ka 2s-1<k1<2s+1-2. Katru kaudzīti, kurā vairāk nekā 2s-1 konfektes (tātad arī kaudzīti, kurā ir k1 konfektes), sadalīsim divās daļās tā, lai vienā daļā būtu 2s-1 konfektes, bet otrā daļā- visas pārējās. Skaidrs, ka neradīsies neviena kaudzīte, kurā ir vairāk nekā 2s-1 konfektes, bet vismaz vienā kaudzītē būs 2s-1 konfektes. Nav svarīgi, kā sadala pārējās kaudzītes: pēc dalīšanas notām iegūsim kaudzītes, kurās katrā ir mazāk 2s-1 konfektes.
Induktīvā pāreja pierādīta.
Aplūkoto risinājumu varēja formulēt arī šādi.
Sadalīsim visus spēles stāvokļus <k1; k2;…; km> divās grupās U un Z. Grupa U sastāv no visiem tiem stāvokļiem, kuriem k1=2l-1 lN. Ievērosim, ka
Induktīvajā pārejā jau pierādījām, ka pēdējie divi apgalvojumi ir patiesi.
No šejienes izriet, ka spēlētājs, kuram
jāizdara gājiens brīdī, kad spēles
stāvoklis ietilpst grupā U, ir uzvarējis,
bet spēlētājs, kuram jāizdara gājiens
brīdī, kad spēles stāvoklis pieder pie
grupas Z ir zaudējis. Tiešām, ja spēlētājam
A jāizdara gājiens brīdī, kad spēles
stāvolkis pieder pie U, viņš var novest
spēli stāvoklī, kas ietilpst zrupā Z;
tad pretiniekam ar savu gājienu (ja viņš to var
izdarīt) noteikti jāatgriežas kādā
stāvoklī no U. Līdz ar to A vienmēr
jāizdara gājiens tikai brīžos, kad spēles
stāvoklis pieder pie U; tā kā <1;
1;…,1> Z, tad A vienmēr varēs
izdarīt gājienus; gājienu pietrūks spēlētājam
B. Ja spēlētājam A jāizdara
gājiens brīdī, kad spēles stāvoklis
pieder pie Z, tad B saņem gājienu,
kad spēles stāvoklis pieder pie U un tad B
pēc pierādītā var uzvarēt.
86. piemērs. Aprakstīsim algoritmu kvadrātsaknes vilkšanai no naturāliem skaitļiem un pierādīsim tā pareizību.
A l g o r i t m a a p r a k s t s. Vispirms tā naturālā skaitļa pieraksta cipari, no kuriem jāvelk kvadrātsakne, jāsadala grupās pa divi, sākot no beigām. (Līdz ar to ciparu grupā skaitļa sākumā būs vai nu viens, vai divi cipari.) Pieņemsim, ka izveidojušās k grupas. Naturālos skaitļus, kuru pieraksts ir izveidotās ciparu grupas, apzīmēsim, sākot no kreisās puses, ar s1, s2, …, sk; s1 ir vai nu viencipara vai divciparu skaitlis, bet s2, …, sk ir divciparu skaitļi. Algoritma darbības rezultātā iegūsim k ciparu skaitli, pie tam tā cipari tiks iegūti secīgi no kreisās uz labo pusi; apzīmēsim šos pagaidām nezināmos ciparus ar c1, c2, …, ck.
Aprakstīsim to iegūšanu ar algoritmu induktīvi.
Bāze. Apskatīsim skaitli s1. Par c1 izvēlēsimies lielāko ciparu, kura kvadrāts nepārsniedz s1; par atlikumu A1 nosauksim starpību
A1=s1-c21.
Pāreja ii+1, ja I<k. Pieņemsim, ka, izmantojot skaitļus s1, s2, …, si, iegūti cipari c1, c2, …, un atlikums ir Ai.
Pierakstīsim atlikumam Ai labajā
pusē skaitli si+1; iegūsim
skaitli 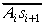
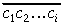
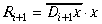
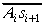
Atlikumu Ai+1 aprēķina
pēc formulas
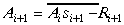 .
.
Kad visas ciparu grupas (to skaits ir k) apstrādātas
un iegūti k cipari, jāpārbauda, vai Ak=0.
Ja Ak=0, tad skaitļa 
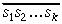
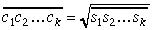
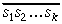
Ilustrēsim algoritma darbību ar diviem piemēriem.
87. piemērs. Atrast 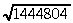
Sadalām zemsaknes skaitļa ciparus grupās tā,
kā norādīts algoritma aprakstā:
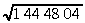
Tā kā s1=1, tad c1=1
un A1=s1-c12=1-1=0.
Pierakstām to šādi
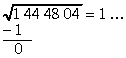
Pierakstot atlikumam A1=0 labajā pusē
ciparu grupu s2=44, iegūstam skaitli 044.
Attēlojam to kā ciparu grupas s2
"nonešanu uz leju":
Reizinot skaitli c1=1 ar 2, iegūstam D2=c12=2.
Pierakstām D2 pa kreisi no skaitļa
044, atdalot tos ar vertikālu svītru:
Lielākais cipars x, ko var pierakstīt skaitlim
D2=2 labajā pusē tā, lai
būtu 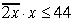
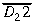
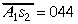
Tātad c2=2 un 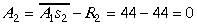
Pēc tam atrodam 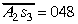
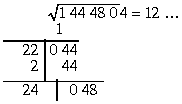
Lielākais cipars x, ko var pierakstīt labajā
pusē skaitlim D3=24 tā, lai būtu
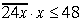
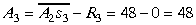
Tālāk atrodam 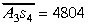
Visas četras ciparu grupas apstrādātas, un
atlikums A4=0. Tāpēc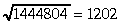
88. piemērs. Atrast 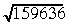
Saskaņā ar algoritmu iegūstam
Visas trīs ciparu grupas apstrādātas, bet atlikums
A30. Tāpēc 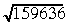
Pārbaudīsim, vai abos apskatītajos piemēros esam ieguvuši pareizu rezultātu.
Nav grūti pārliecināties, ka 12022=1444804.
Tātad 87. piemērā ar aplūkoto algoritmu
ir iegūts pareizs rezultāts. Tāpat nav grūti
pārliecināties, ka 3992=159201 un 4002=
160 000, tātad
Tā kā 159636 atrodas starp divu naturālu kaimiņu skaitļu kvadrātiem, tad tas nav naturāla skaitļa kvadrāts. Tātad arī 88. piemērā ar aplūkoto algoritmu iegūtais rezultāts ir pareizs.
Kāda situācija izveidojusies?
Esam aprakstījuši algoritmu, kuru var pielietot jebkuram naturālam skaitlim. Skaidrs, ka veicamo darbību skaits katram naturālam skaitlim ir galīgs, jo jāapstrādā visas ciparu grupas, bet to skaits ir galīgs. Mēs arī apgalvojām, ka ar algoritmu iegūtais skaitlis ir kvadrātsakne no dotā skaitļa, ja pēdējais atlikums ir 0; ja pēdējais atlikums nav 0, tad no dotā skaitļa kvadrātsakni naturālos skaitļos izvilkt nevar. Esam arī pierādījuši, ka šis apgalvojums ir patiess divos atsevišķos gadījumos.
Vai teiktais nozīmē, ka šis apgalvojums ir patiess arī visos citos gadījumos, t.i., ka, rīkojoties aprakstītajā veidā par katru naturālu skaitli var noskaidrot, vai tam eksistē naturāla kvadrātsakne vai ne, un, ja eksistē, tad to var atrast? Protams, ka, nē! No tā, ka vispārīgs apgalvojums ir patiess vairākos atsevišķos gadījumos, nevar secināt, ka tas ir patiess vienmēr - arī citos gadījumos.
Pierādīsim, ka ar aplūkoto algoritmu par katru naturālu skaitli var noskaidrot, vai šim skaitlim eksistē vai neeksistē naturāla kvadrātsakne; ja šāda kvadrātsakne eksistē, tad, izmantojot algoritmu, to var aprēķināt. Pierādīsim vispārīgāku teorēmu; vajadzīgais apgalvojums būs tā secinājums.
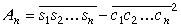 .
.
Iedomāsimies uz brīdi, ka teorēma pierādīta.
Ja n=k, iegūsim šādu secinājumu.
Kad skaitļa 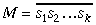
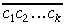
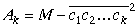
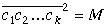
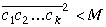
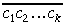
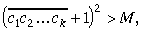
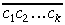
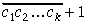
Atliek pierādīt 6. teorēmu.
6. teorēmas pierādījums ideju ziņā ir vienkāršs, bet tehniski sarežģīts, tāpēc tā izpratnē var rasties grūtības. Tomēr ieteicam lasītājam censties to apgūt. Matemātikā iespējamas divu veidu grūtības: principiālas, kas saistītas ar jaunu ideju izvirzīšanu un uztveršanu, un tehniskas, kas saistītas ar šo ideju realizēšanu. Radošam darbam matemātikā galvenokārt nepieciešamas spējas pārvarēt pirmā veida grūtības; bet, lai šīs spējas varētu pilnā mērā izpausties, nepieciešams virtuozi pārvaldīt dažādus tehniskus paņēmienus, spēt viegli pārvarēt nebūtiskus šķēršļus, lai varētu koncentrēt uzmanību un spēkus galveno uzdevumu veikšanai. Raugoties no šāda viedokļa, turpmāk aplūkoto pierādījumu var salīdzināt ar sarežģītu pirkstu vingrinājumu, gammu un akordu sēriju pianista apmācības procesā, un šī pierādījuma izparatne liecina par diezgan augstu lasītāja matemātisko kultūru.
Kā būtu visdabiskāk pierādīt 6. teorēmu? Šī teorēma runā par stāvokļiem, kādi rodas algoritma izpildes procesā, apstrādājot vispirms vienu, pēc tam otru, …, n-to, …ciparu grupu. Tāpēc pats dabīgākais ceļš- izdarīt indukciju pēc ciparu grupu skaita n.
Bāze. Ja n=k, teorēmā izteiktais apgalvojums ir patiess; tas tieši izriet no algoritma bāzes apraksta.
Pāreja nn+1, ja n<k. Pieņemsim,
ka teorēmas apgalvojums ir patiess, ja skaitļa 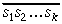
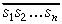 ,
t.i.,
,
t.i.,
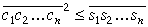 |
(1) |
un
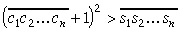 | (2) | |
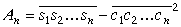 . . | (3) | |
Nevienādība (2) seko no tā, ka 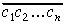
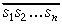
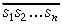
Pēc tam saskaņā ar algoritmu aprēķina
skaitli
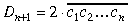 | (4) | |
un atrod vislielāko no tiem cipariem x, kas apmierina
nevienādību
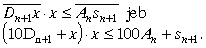 | (5) | |
Vislielāko ciparu x, kas apmierina nevienādību (5), izvēlas par cn+1.
Atradīsim nevienādības, kas raksturo ciparu
cn+1. Tā kā cn+1
apmierina nevienādību (5), tad
| (6) | |
Ja cn+1+1 ir cipars, tad cn+1+1
neapmierina vienādību (5), jo cn+1-
lielākai no cipariem x, kas apmierina (5); tad pareiza
ir nevienādība
| (7) | |
Pierādīsim, ka nevienādība (7) pareiza
tarī tad, ja cn+1+1=10, t.i.,
| (8) | |
No sakarībām (3), (4) un (8 ) iegūstam nevienādībai
(8) ekvivalentu nevienādību
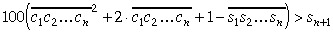 | (9) | |
jeb
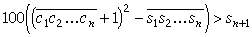 | (10) | |
Izmantojot nevienādību (2), secinām, ka nevienādības (10) kreisajā pusē atrodas skaitlis, kas nav mazāks par 100. Tā kā sn+1 ir divciparu skaitlis, tad nevienādība (10) pierādīta.
Tātad nevienādība (7) pareiza visām iespējamām cn+1 vērtībām.
Lai izdarītu induktīvo pāreju, jāpierāda, ka
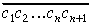 ir lielākais naturālais
skaitlis, kura kvadrāts nepārsniedz
ir lielākais naturālais
skaitlis, kura kvadrāts nepārsniedz 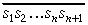 ;
;
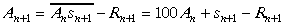 , , | (11) |
apmierina vienādību
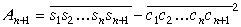 | (12) | |
Pierādīsim vispirms vienādību (12). Tiešām,
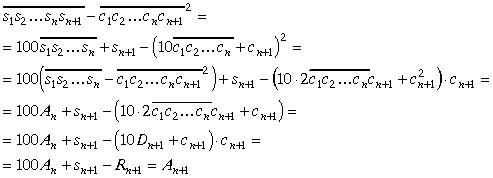
(pārveidojumos izmantotas vienādības (3), (4) un (11) un Rn+1 definīcija).
Acīmredzot pierādāmo apgalvojumu a) var izteikt
ar šādām divām nevienādībām
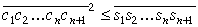 | (13) | |
un
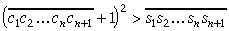 | (14) | |
Pārbaudīsim vai nevienādība (13) ir pareiza:
ko arī vajadzēja pierādīt (pārvietojumos izmantotas sakarības (4), (6) un (3)).
Pārbaudīsim vienādību (14)
ko arī vajadzēja pierādīt (pārveidojumos izmantotas sakarības (7) un (3)).
Induktīvā pāreja un līdz ar to arī 6. teorēma pierādīta.
50. zīmējumā attēlota 6. teorēmas induktīvās pārejas loģiskā shēma.
Atzīmēsim, ka abos šajā nodaļā
aplūkotajos piemēros tika pierādīts spēcīgāks
apgalvojums nekā tas, kas nepieciešams algoritma pareizības
konstatēšanai. Tā otrajā piemērā
pierādījām arī apgalvojuma par atlikumu
An vērtībām, t.i., izmantojām
metodi, kas tika aplūkota 6. nodaļā.

50. zīm.
Uzdevumi paškontrolei XI
171. Akmeņu kaudzē ir n akmeņu. Divi spēlētāji pēc kārtas ņem no tās akmeņus. Spēlētājs, kurš izdara pirmo gājienu, nedrīkst pirmajā gājienā paņemt visus akmeņus; katrā tālākajā gājienā drīkst paņemt ne vairāk akmeņu, kā iepriekšējā gājienā paņēmis pretinieks. Uzvar tas, kurš paņem pēdējo akmeni. Kā jāspēlē, lai uzvarētu?
172. Analizēt iepriekšējo spēli, ja otrais nosacījums aizstāts ar šādu: katrā no tālākajiem gājieniem drīkst paņemt ne vairāk kā dubultotu akmeņu skaitu, kurus iepriekšējā gājienā paņēmis pretinieks.
173. Akmeņu kaudzē n akmeņu. Divi spēlētāji pēc k; kārtas ņem no tās akmeņus. Visus kaudzē palikušos akmeņus drīkst paņemt tikai tad, ja akmeņu skaits kaudzē nepārsniedz iepriekšējā gājienā pretinieka paņemto akmeņu skaitu; citādu ierobežojumu nav. Uzvar tas, kurš paņem pēdējo akmeni. Kā jāspēlē, lai uzvarētu?
174. Spēlētāja A rīcībā ir 1 km garš taisnes nogrieznis - "banka". Spēlētājs drīkst dot spēlētājam A glabāšanā dažādus mazus taisnes nogrieznīšus, ievērojot šādus nosacījumus:
a) nogriežņus var nodot glabāšanā un pieprasīt atpakaļ jebkurā laikā un jebkurā kārtībā;
b) katrs glabāšanā nodotais taisnes nogrieznis jānovieto uz 1 km garā nogriežņa , un to nedrīkst pārvietot līdz brīdim, kad spēlētājs B to pieprasa atpakaļ;
c) nekādiem diviem taisnes nogrieznīšiem, kas novietoti uz nogriežņa un vēl nav pieprasīti atpakaļ, nedrīkst būt kopēju punktu;
d) katrā laika momentā spēlētājs B zina, kurā vietā uz nogriežņa novietots katrs glabāšanā nodotais uzgrieznītis;
e) nevienā laika momentā glabāšanā nodoto nogrieznīšu garumu summa nepārsniedz 1 mm.
Pierādīt, ka spēlētājs B var nodot spēlētājam A glabāšanā nogriežņus un pieprasīt tos atpakaļ tādā kārtībā, ka spēlētājs A pēc galīga soļu skaita nevarēs uz nogriežņa novietot pusmilimetru garu nogriezni.
175. Dotas 2n-1 dažādas masas monētas. Mēs zinām, kura monēta smagākā, kura- otrā smagākā utt. Bez tam mūsu rīcībā ir sviras svari bez atsvariem un vēl viena monēta, par kuras masu ir zināms tikai, ka tā atšķiras no visu pārējo monētu masām. Pierādīt, ka ar n svēršanām iespējams noteikt, par kurām no dotajām monētām šī 2n-tā monēta ir vieglāka, bet par kurām- smagāka.
176. Dotas n dažādas masas monētas un sviras svari ar atsvariem. Pierādīt, ka ar n[log2n] svēršanām iespējams sakārtot monētas masu augšanas secībā..
178. Pieņemsim, ka, pastāvot 176. uzdevuma nosacījumiem, mums jāatrod tikai viena pati k-tā smagākā monēta (k=1, 2, …, n). Pierādīt, ka to var izdarīt, izmantojot ne vairāk kā 15n-163 svēršanas, ja n>32.
*178. Pierādīt, ka naturālos skaitļus
no 1 līdz 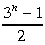
ĪSS LITERATŪRAS APSKATS.
Matemātiskām spēlēm veltīta ļoti plaša literatūra (sk., piemēram, [35], [40] un tur norādītos darbus); tomēr pierādījumi parasti nav tik stingri, kā tas darīts 85. piemērā. Ieteicam lasītājam katru spēli, ko viņam izdodas izanalizēt "intuitīvi", aprakstīt arī precīzi, izmantojot matemātisko indukciju.
Par jautājumiem, kas saistīti ar algoritmu un programmu pareizības pierādīšanu, sk., piemēram [11], 42.-45. Un 48. lpp., [49], 362.-365., 372., 388. lpp.
175.-177. uzdevumi saistīti ar informācojas kārtošanas problēmām, kurām mūsdienu skaitļošanas tehnikas izmantošanā ir ārkārtīgi svarīga nozīme. Labākā grāmata, kurā ir arī daudz uzdevumu, ir [50].
Indukcijas pielietojums dažādu shēmu konstruēšanā un to pareizības pierādījumos var atrast rakstos [51] un [52].
178. uzdevumu var vispārināt šādi:
kāds ir maksimālais skaitlis f(n), kuram
visus naturālos skaitļus no 1 līdz f(n)
var sadalīt grupās tā, ka nekādu divu
vienas grupas skaitļu starpība nav no šīs
pašas grupas? 178. uzdevumā risinājums parāda,
ka 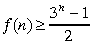
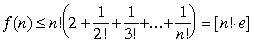 .
.
Zināmas ir tikai šādas f(n) vērtības:
f(1)=1, f(2)=4, f(3)=13, f(4)=44;
nedaudz uzlabot 178. uzdevumā doto apakšējo
novērtējumu palīdz nevienādība
Piemēram, par f(5) zināms, ka 133f(5)327.
Jebkāds progress f(n) vērtību
atrašanā vai robežu precizēšanā
būtu ievērojams matemātisks sasniegums.

| 
| 
| 
| 
|