12. NODAĻA

DAŽĀDI INDUKCIJAS METODES PIELIETOJUMI

Matemātisko indukciju bieži var pielietot neiespājamības pierādījumos.

89. piemērs. Dotas x vienāda izskata monētas. Tām visām, izņemot vienu, ir vienāda masa, bet viena ir smagāka nekā pārējās. Cik sver katra monēta un par cik atšķiras smagākās monētas masa no pārējo monētu masas, nav zināms. Doti arī sviras svari bez atsvariem; uz katra svaru kausa var uzlikt jebkuru daudzumu monētu. Svari rāda tikai to, uz kura kausa uzlikts lielāks smagums, bet ne to, par cik viens kauss smagāks nekā otrs; ja uz kausiem uzlikatas vienādas masas, tie atrodas līdzsvarā. Pierādīt, ka ar n svēršanām uz šādiem svariem nevar noskaidrot, kura no x monētām ir smagākā, ja x>3ⁿ.

Arī tad, ja zināms, ka starpība starp smagākās un vieglākās monētas masām mazāka nekā vieglākās monētas masa, ar n svēršanām nevar noskaidrot, kura monēta ir smagākā.

Pierādīsim to ar indukciju pēc n.

Bāze. Ja n=0, tad x>3⁰=1.

Skaidrs, ka bez svēršanas (n=0) nevar noskaidrot, kura no x monētām (x>1) ir smagākā.

Pāreja. kk+1. Pieņemsim, ka ar k svēršanām nevar noskaidrot, kura no x monētām ir smagākā, ja x>3^k. Izraudzīsimies y>3^k+1 un pierādīsim, ka ar k+1 svēršanām nav iespējams noskaidrot, kura no y monētām ir smagākā.

Pieņemsim pretējo, ka ir tāda metode, ar kuru, izdarot k+1 svēršanas, starp y monētām var atrast smagāko monētu.

No induktīvās hipotēzes izriet, ka pirmajā svēršanā uz svaru kausiem jāliek vienāds skaits monētu. Tiešām, ja uz viena svaru kausa uzlikts vairāk monētu nekā uz otra kausa, tad pirmais kauss nosveras uz leju tāpēc, ka starpība starp smagākās un vieglākās monētas masu ir mazāka nekā vieglākās monētas masa. Ar šo svēršanu neiegūstam nekādu informāciju par smagāko monētu, jo smagākā monēta var atrasties gan uz pirmā svaru kausa, gan uz otrā svaru kausa, gan starp tām monētām, kas nav uzliktas uz svaru kausiem. Tātad šādu svēršanu var atmest. Bet tad smagāko no y (y>3^k+1>3^k) monētām var noteikt ar atlikušajām k svēršanām, kas ir pretrunā ar induktīvo hipotēzi.

Tātad uz abiem svaru kausiem jāliek vienāds skaits monētu.

Apzīmēsim uz katra no savru kausiem uzlikto monētu skaitu ar A, bet atlikušo monētu skaitu ar B. Tā kā 2A+B=y>3^k+1, tad vai nu A>3^k, vai arī B>3^k. Tiešām, ja A3^k un B3^k, tad y=2A+B=y>33^k=3^k+1, kas ir pretrunā ar y izvēli.

Tālāk aplūkosim divus gadījumus:

1. A>3^k.

Iekams uzliekam monētas uz svaru kausiem, mums nav nekādas informācijas par to, kura no y monētām varētu būt smagākā. Tāpēc var gadīties (stratēģijā tam jābūt paredzētam), ka smagākā monēta ir starp tām, kas uzliktas uz svaru kausiem. Bet tad pēc pirmās svēršanas ir skaidrs, ka smagākā monēta var būt jebkura no A monētām, kas uzliktas uz smagākā svaru kausa.Tā kā viena svēršana jau izdarīta, tad šī smagākā monēta jāatrod ar k svēršanām. Bet to, pēc induktīvā pieņēmuma, nevar izdarīt, jo A>3^k,

1. B>3^k.

Ja svaru kausi stāv līdzsvarā, tad pēc pirmās svēršanas skaidrs, ka smagākā monēta var būt jebkura no atlikušajām B monētām. Pēc induktīvā pieņēmuma to nevar atrast ar neizmantotajām svēršanām, jo B>3^k. Tātad smagāko no y (y>3^k+1) monētām nevar atrast ar k+1 svēršanām.

Induktīvā pāreja izdarīta.

Spriedumus, kas ļoti līdzīgi induktīvajai pārejai, bieži lieto, lai pierādītu, ka kāda kopa vai skaitļu virkne ir bezgalīga (vai arī, ka eksistē bezgalīga kopa vai skaitļu virkne ar vajadzīgajēm īpašībām).

90. piemērs. Pierādīt, ka vienādojumam x²-2y²=1 eksistē bezgalīgi daudz atrisinājumu naturālos skaitļos.

Viegli redzēt, ka šim vienādojumam eksistē atrisinājums naturālos skaitļos: (x; y)=(3;2).

Pieņemsim, ka (a; y) ir dotā vienādojuma atrisinājums naturālos skaitļos; tas nozīmē, ka

a22b2=1.

(1)

Kāpinot vienādības (1) abas puses kvadrātā, iegūstam

a^4-4a²b²+4b⁴=1

a⁴+4a²b²+4b⁴-8a²b²=1,

(a²+2b²)²-2(2ab)²=1.

Redzam, ka arī skaitļu pāris (a²+2b²; 2ab) apmierina doto vienādojumu. Tātad no pirmā atrisinājuma (3;2) varam iegūt jaunu atrisinājumu (3²+22², 232)=(17;12), no tā- atkal jaunu atrisinājumu utt. Skaidrs, ka šajā atrisinājumu virknē neviens atrisinājums neatkārtojas, jo a²+2b²>a un 2ab>b, tāpēc visi šīs virknes skaitļu pāri ir dažādi.

91. piemērs. Pierādīt, ka eksistē cik patīk garas virknes a₁, a₂, …, a_n, kuru locekļi ir 0 vai 1, ar īpašību, ka katram naturālam k, 0kn-1, summa a₁a_k+1+a₂a_k+2+…+a_n-1a_n ir nepāra skaitlis.

Viegli redzēt, ka šāda virkne eksistē, ja n=4. Tāda ir, piemēram,virkne 1101. uzdevumā minēto virkņu eksistence izriet no šāda apgalvojuma: ja n ciparu virkne A apmierina uzdevuma prasības, tad šīs prasības apmierina arī 7n-3 ciparu virkne.

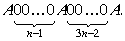
Pierādījumā jāšķiro gadījumi, kad 0k+,n-1, nk3n-2, 3n-1k6n-4,

6n-3k7n-4.

Tādejādi no virknes ar 4 locekļiem varam iegūt ar 74-3=25 locekļiem, no tās savukārt virkni ar 725-3=172 locekļiem utt.

No pierādītā nevar secināt (uzdevumā tas arī nav prasīts), ka eksistē bezgalīga virkne ar īpašību, ka katram k0 summa a₁a_k+1+a₂a_k+2+a₃a_k+3 …(šī bezgalīgā summa jāsaprot kā summas a₁a_k+1+a₂a_k+2+…+ a_n-1a_n robeža, kad ir nepāra skaitlis: no tā, ka eksistē cik patīk garas skaitļu virknes ar kādu noteiktu īpašību, vēl neizriet, ka eksistē bezgalīga skaitļu virkne ar tādu pašu īpašību. Atcerieties 129. uzdevuma risinājumu: nevienā no konstruētajām skaitļu klasēm neietilpa bezgalīga augoša aritmētiska progresija, bet katra no tām saturēja cik patīk garas galīgas augošas aritmētiskas progresijas.

Jautājums, kādos gadījumos no tā, ka eksistē cik patīk lielas kopas ar kādu noteiktu īpašību, izriet bezgalīgas kopas eksistence, kurai ir tāda pati īpašība, ir sarežģīts, un to risina ar matemātiskās loģikas metodēm.

Uzdevumi paškontrolei XII

179. Dota kaste ar cukuru, sviras svari un atsvars, kura masa ir 1 g. Pierādīt, ka ar n svēršanām uz šiem svariem nevar nosvērt vairāk kā 2ⁿ-1 gramus cukura.

180. n monētas sakārtotas masu pieaugšanas secībā, bet n+1-tās monētas masa atšķiras no visu pārējo n monētu masām. Izmantojot sviras svarus bez atsvariem, noteikt, kurā vietā šī monēta jānovieto doto n monētu rindā, lai visu n+1 monētu rinda būtu sakārtota masu pieaugšanas secībā.

Pierādīt, ka to nevar izdarīt ar k svēršanām, ja n2^k. (Uz kausiem drīkst likt tikai pa vienai monētai.)

181. Dotas 3 vertikālas asis A, B un C (51. zīm.). Uz ass A atrodas n diski: apakšējais disks ir vislielākais, katrs nākošais disks mazāks nekā iepriekšējais. Diski jāpārliek uz ass C, izmantojot asi B. Ar vienu gājienu drīkst pārlikt tikai vienu disku; nedrīkst likt lielāku disku uz mazāka.

Cik gājienu nepieciešams, lai to izdarītu?

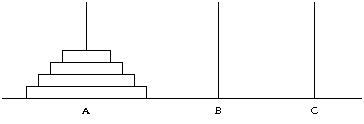
51. zīm.

182. Pierādīt, ka pirmskaitļu ir bezgalīgi daudz.

183. Pierādīt, ka dažādu pirmskaitļu, ar kuriem dalās polinoma 2x²+2x+1 vērtības, kur x=1, 2, …, n, …, ir bezgalīgi daudz.

184. Pierādīt, ka, pieaugot n vērtībai, izteiksmes 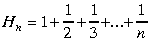vērtība var kļūt lielāka par jebkuru iepriekš dotu pozitīvu skaitli (t.i., pierādīt, ka H_{n, ja} n).

185. Tuksneša malā atrodas neierobežots pārtikas un ūdens daudzums. Cilvēks var nest sev līdzi pārtiku un ūdeni vienai dienai, turklāt gan pārtiku, gan ūdeni viņš patētē regulāri vienādos daudzumos. Tuksnesī var izveidot pārtikas un ūdens noliktavas (pieņemsim, ka pārtiku tajās neviens dzīvnieks neapēd, tā nebojājas un ūdens neiztvaiko). Pierādīt, ka cilvēks var ieiet tuksnesī cik patīk tālu un atgriezties atpakaļ.

186. Dots neierobežots daudzums vienādu homogēnu ķieģeļu. Mēs vēlamies tos sakraut citu virs cita tā, lai augšējā ķieģļa tālākās malas projekcija atrastos vismaz attālumā s km no apakšējā ķieģeļa (sk. 52. zīm.); turklāt ķieģeļus savā starpā nekādi nedrīkst sastiprināt, bet konstrukcija nedrīkst sagāzties.

Pierādīt, ka to var izdarīt katram s.

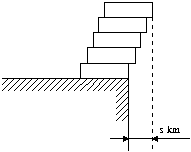
52. zīm.

187. Pierādīt, ka no cipariem 1 un 2 var izveidot cik patīk garas virknes, kurās neviena ciparu grupa neatkārtojas trīs reizes pēc kārtas

188. Pierādīt, ka no cipariem 1, 2, 3 un 4 var izveidot cik patīk garas virknes, kurās neviena ciparu grupa neatkārtojas divas reizes pēc kārtas

189. Pierādīt, ka eksistē tāda dažādu naturālu skaitļu virkne, ka katru naturālu skaitli var izteikt vienā vienīgā veidā ar šīs virknes elementu starpību.

Turpmākie uzdevumi nav saistīti ar šajā paragrāfā apskatītajiem piemēriem, bet parāda matemātiskās indukcijas pielietojumus loģiska rakstura uzdevumu risināšanā.

190. n cilvēki sēž rindā cits aiz cita. Katrs redz visus sev priekšā sēdošos (tātad tas, kurš sēž pašā priekšā, neredz nevienu). Šiem cilvēkiem skaļi paziņo, ka viņiem galvās tiks uzliktas cepures: viena balta un n-1 melnas. Pēc tam nodzēš gaismu un tā arī izdara. Kad gaismu atkal iededz, kāds cilvēks B jautā pēc kārtas visiem rindā sēdošajiem, sākot ar pēdējo: "Vai jūs zināt, kāda cepure jums galvā?" Atbilde "jā" vai "nē" tiek pateikta skaļi. Kādos gadījumos cilvēks, kuram galvā ir baltā cepure, pateiks "jā"?

191. Iepriekšējā uzdevuma apstākļos cilvēkiem paziņo, ka viņiem galvā uzliks cepures no komplekta, kurā ir n baltas un n-1 melnas cepures. Pārējie nosacījumi mainās. Vai atradīsies cilvēks, kas uz cilvēka B jautājumu atbildēs "jā"?

192. Istabā atrodas n cilvēki. Tiek nodzēsta gaisma. Spēles vadītājs B katram cilvēkam pieskaras pie pieres ar mitru otiņu; dažos gadījumos tā samērcēta ūdenī, citos- melnā krāsā. Pēc tam gaisma tiek ieslēgta. Istabā nav spoguļu, un cilvēki nedrīkst sarunāties vai kā citādi informēt cits citu, bet drīkst brīvi staigāt un apskatīt viens otru. Vadītājs B paziņo: "Dažiem no jums piere ir nosmērēta ar krāsu. Ik pēc stundas uz piecām minūtēm tiks atslēgtas istabas durvis, un tie, kas vēlēsies, varēs aiziet nomazgāties."

Pierādīt: ja k cilvēkiem pieres nosmērētas ar krāsu, tad tieši pēc k stundām visi cilvēki ir mazgāties. Mēs pieņemam, ka viņi ir "absolūti gudri".)

193. Kā mainīsies iepriekšējā uzdevumā aprakstītā situācija, ja vadītājs B izlaidīs teikuma daļu "dažiem no jums piere ir nosmērēta ar krāsu"? Intuitīvi skaidrs, ka mazgāties neies neviens: bet, ja k2, visi zina, ka kādam piere nosmērēta ar krāsu, tātad šī vadītāja B teikuma daļa it kā nemaz nav nepieciešama. Vai tas nav pretrunā ar 192. uzdevuma apgalvojumu?

194. Spēlē piedalās divi cilvēki A₁ un A₂ un vadītājs B. Vadītājs uzraksta spēles dalībniekiem A₁ un A₂ uz pierēm divus naturālus blakus skaitļus: vienam n, otram n+1. Katrs no cilvēkiem A₁A₂ redz skaitli, kas uzrakstīts uz pieres otram, bet nevar ieraudzīt savu skaitli; viņi vienīgi zina, ka abi uzrakstītie skaitļi ir viens otram sekojoši naturāli skaitļi. Pēc tam vadītājs pārmaiņus prasa dalībniekiem A₁ un A₂, sākot ar A₁: "Vai jūs zināt, kāds skaitlis uzrakstīts jums uz pieres?"

Vai kāds no spēles dalībniekiem A₁, A₂ atbildēs "jā"?

Apskatītajos piemēros un uzdevumos matemātiskā indukcija bija galvenā pierādīšanas metode. Tomēr redzējām, ka rezultātus, kurus iegūst ar matemātisko indukciju, var iegūt arī bez tās (piemēram, 32. uzdevums). Varbūt visus rezultātus matemātikā var iegūt, nelietojot matemātiskās indukcijas metodi?

Lai atbildētu uz šo jautājumu, jāiedziļinās matemātiskās indukcijas struktūrā. Stingrā aksiomātiskā izklāstā visas matemātikas nozares tiek reducētas uz aritmētiku. Starp aritmētikas aksiomām savukārt ir aksioma- matemātiskās indukcijas princips. Līdz ar to ir skaidrs, ka matemātisko indukciju ne tikai nevar izslēgt no matemātikas, bet tā ir viens no matemātikas pamatu pamatiem. Īstenībā pat nevienā daudzmaz sarežģītā pierādījumā, ja to gribētu izklāstīt pilnīgi precīzi, nevar iztikt bez matemātiskās indukcijas izmantošanas. Par to, cik dziļi matemātiskā indukcija "ieaudusies" visā matemātikā, liecina šādi piemēri.

92. piemērs. 7. paragrāfā 67. piemērā un 140.-142. uzdevumā pierādījām t.s. Ramseja skaitļu eksistenci. Izrādās, ka, tikai ļoti nedaudz izmainot matemātiskās indukcijas aksiomu aritmētikas aksiomu sarakstā, Ramseja skaitļu eksistenci vairs nav iespējams pierādīt- var "uzbūvēt" tādu aritmētiku, kas apmierina visas pārējās aksiomas un izmainīto (pavājināto) indukcijas aksiomu, bet kurā Ramseja skaitļi neeksistē- uz šīs aritmētikas bāzes veidotajā ģeometrijā var atrast tādu krāsu skaitu k un virsotņu skaitu v, ka cik patīk daudzus punktus n var savienot pa pāriem ar līniju un katru līniju novilkt vienā no k krāsām tā, ka nebūs v punktu, kas visi savā starpā savienoti ar vienas krāsas līnijām.

93. piemērs. Plaši pazīstama ir šāda neatrisināta matemātiska problēma: vai eksistē bezgalīgi daudz pirmskaitļu kas, izsakāmi formā n²+1, kur n- naturāls skaitlis?

Izrādās, ka, nedaudz pavājinot matemātikas indukcijas aksiomu, var konstuēt tādu aritmētiku, kurā šādu pirmskaitļu ir bezgalīgi daudz; šī apgalvojuma pierādījums nebūt nav sevišķi sarežģīts.

94. piemērs. No senās Grieķijas laikiem pazīstama šāda slavena neatrisināta problēma: vai eksistē bezgalīgi daudzi tādi pirmskaitļi p, ka p+2 arī ir pirmskaitlis? (Tādus pirmskaitļus p un p+2 sauc par dvīņu pirmskaitļiem; piemēram, dvīņu pirmskaitļu pāri ir 3 un 5, 5 un 7, 11 un 13, 17 un 19 utt.)

Nedaudz pavājinot matemātiskās indukcijas aksiomu, var izveidot tādu aritmētiku, kurā dvīņu pirmskaitļu pāru ir bezgalīgi daudz. Pavājinot indukcijas aksiomu, var arī izveidot citu aritmētiku, kurā dvīņu pirmskaitļu pāru ir tikai galīgs skaits. Tātad aritmētikā ar pavājināto indukcijas aksiomu jautājums pat to, vai šādu pāru ir tikai galīgs skaits, nav atkarīgs no matemātikas aksiomām; saglabājot matemātiskās indukcijas aksiomu nemainītu, šī problēma ir ārkārtīgi sarežģīta. (Iespējams, ka atbilde uz šo jautājumu nav atkarīga arī no aksiomu sistēmas, kas satur nepavājināto indukcijas aksiomu.)

Raugoties no šāda viedokļa, 1.-5. teorēma par citām indukcijas shēmām pilnīgi precīzā izklāstā būtu jāpierāda ar MIP. Un, tā kā tās var pierādīt ar MIP, tad iegūstam šādu rezultātu:

visus apgalvojumus, ko var pierādīt, atsaucoties uz 1.-5. teorēmu (arī visus apgalvojumus, kas pierādīti šajā grāmatā), var pierādīt arī tieši ar MIP.

Tātad 1.-5. teorēmas var uzskatīt nevis par spēcīgākiem apgalvojumiem nekā MIP (kā varētu likties pirmajā acumirklī), bet tikai par indukcijas aksiomas formulējuma variantiem, kas dažu apgalvojumu pierādīšanā ir ērtāki (bet ne spēcīgāki!) kā MIP.

Matemātikā lieto arī citus indukcijas aksiomas formulējuma variantus. Lūk, viens no tiem.

7. teorēma (indukcija pēc reizinājuma).

Dots: A(n)- vispārīgs apgalvojums , kas satur parametru n (n- naturāls skaitils).

Šo teorēmu var arī pierādīt pamatojoties uz matemātiskās indukcijas principu. Tās pielietojumus sk. 195.-197. uzdevumā. Par citiem, vēl vispārīgākiem matemātiskās indukcijas principa formulējumiem (kas satur kā speciālgadījumus visus jau apskatītos formulējumus) sk. [11] 49.-50. lpp. un [53] 28.-29. lpp.

Nobeigumā jāatzīmē, ka matemātiķi nebūt ne katru savu soli pašā pētniecības procesā pamato ar matemātisko indukciju. Katram no viņiem ir izveidojies noteikts intuitīvs priekšmets, kādos gadījumos precīzu pierādījumu ar indukciju var aizstāt ar vārdiem "un tā tālāk", nenonākot pie nepareiziem rezultātiem, apmēram tāpat, kā mēs, ievērojuši, ka aritmētiskajā progresijā a₂=a₁+d, a₃=a₁+2d, a₄=a₁+3d, sakām " un tā tālāk, a_n=a₁+(n-1)d." Šo priekšstatu matemātiķi arī bieži izmanto. Tomēr, noformējot sava darba rezultātus (zinātniskā rakstā, monogrāfijā utt.), matemātiķis šādus "baltos plankumus" aizpilda ar precīziem pierādījumiem vai arī īsi norāda, kādā veidā šie pierādījumi izdarāmi. Matemātisko indukciju pašā pētniecības procesā lieto tādos gadījumos, kad pētnieks vēl intuitīvi nejūt, ar kādiem spriedumiem apskatāmajā jautājumu lokā iegūstami pareizi rezultāti, ar kādiem- nepareizi.

195. Doti 2n-1 naturāli skaitļi, starp tiem var būt arī vienādi. Pierādīt, ka no šiem skaitļiem var izvēlēties tieši n skaitļus, kuru summa dalās ar n.

196. Pierādīt, ka to naturālo skaitļu skaits, kas mazāki nekā dotais naturālais skaitlis n un kuriem ar n lielākais kopīgais dalītājs ir 1, ir

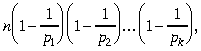
kur p₁, p₂, …, p_k- visi dažādie pirmskaitļi, ar kuriem dalās n (Eilera formula).

1. Pieņemsim, ka n- naturāls skaitlis, d₁, d₂,…, d_k- visi dažādie skaitļa n naturālie dalītāji, a_i-skaitļa d₁ naturālo dalītāju skaits (i=1, 2, …, k). Pierādīt, ka

Beigas